Эволюция геометрии: путь от древних измерений до современной науки

Геометрия как наука зародилась в глубокой древности, став одним из первых проявлений человеческой мысли, направленной на познание окружающего мира. Слово «геометрия» происходит от греческого «γεωμετρία», что буквально означает «измерение земли». Это происхождение термина неслучайно – первые геометрические концепции возникли именно из необходимости решения практических задач.

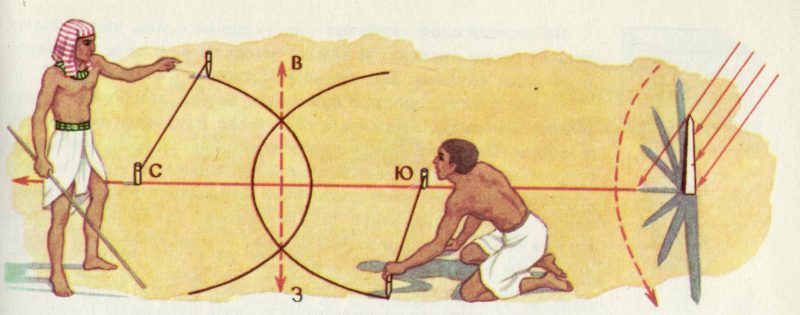
Древнейшие цивилизации – египтяне, вавилоняне, индийцы и китайцы – независимо друг от друга начали развивать элементарные геометрические представления еще более 4000 лет назад. В Древнем Египте регулярные разливы Нила заставляли земледельцев заново размечать границы своих участков после каждого паводка. Эта необходимость привела к развитию методов измерения площадей и построения прямых углов.

Первый этап развития геометрии (до V века до н.э.) характеризовался накоплением эмпирических знаний. Люди учились находить расстояния между предметами, определять размеры участков земли и ориентироваться по расположению различных объектов. Вавилоняне уже тогда знали теорему Пифагора для некоторых частных случаев и могли вычислять площади основных геометрических фигур.

Античный период и систематизация знаний

Особое место в истории геометрии занимает Древняя Греция V-III века до н.э., когда произошел качественный скачок от практической геометрии к теоретической науке. Именно в этот период появились первые математические школы, где геометрия стала рассматриваться как абстрактная дисциплина.

Греческий математик Евклид в своих «Началах» систематизировал все известные к тому времени геометрические знания и создал первую аксиоматическую теорию.

Важным этапом развития геометрии стало ее применение в архитектуре и строительстве. Уже в древности геометрия стала основой для организации пространства и времени, землеустройства и возведения сложных сооружений.

Греческие архитекторы использовали геометрические принципы при проектировании храмов и общественных зданий, что способствовало дальнейшему развитию науки.

Средневековый период и его особенности

Средневековый период (примерно V–XV века) стал временем, когда геометрия переживала своеобразный «перерыв» в Европе. Однако это не означало полного застоя в развитии науки. Напротив, именно в этот период арабские ученые сыграли ключевую роль в сохранении и дальнейшем развитии геометрического знания.

Арабские математики перевели на свои языки труды древнегреческих авторов, таких как Евклид, Архимед и Аполлоний. Эти переводы стали мостом между античной наукой и европейским Возрождением. Особое значение имели комментарии и дополнения к этим работам. Например:

• Аль-Хорезми (780–850) написал трактаты по астрономии и геометрии, которые позже были переведены на латинский язык и оказали влияние на европейскую науку.
• Табит ибн Курра (836–901) внес значительный вклад в развитие тригонометрии, которая стала важным инструментом для астрономических расчетов.
• Омар Хайям (1048–1131), известный не только как поэт, но и как математик, исследовал геометрические методы решения алгебраических уравнений.

Арабские ученые также ввели новые понятия и развивали прикладные аспекты геометрии. Например, они разработали более точные методы измерения углов и расстояний, что было важно для навигации, картографии и строительства.

В Европе интерес к геометрии начал возрождаться только к XII–XIII векам, благодаря переводам арабских текстов на латинский язык. Университеты, такие как Парижский и Оксфордский, стали центрами изучения геометрии. В этот период начали активно использовать геометрические принципы в архитектуре, особенно в строительстве готических соборов.

Готическая архитектура требовала точных расчетов для создания высоких сводов, арок и витражей. Здесь геометрия служила не только теоретическим основанием, но и практическим инструментом.

Эпоха Возрождения (XIV–XVI века) стала временем, когда геометрия получила новый импульс развития. Это был период, когда искусство и наука начали сближаться, а геометрия стала основой для многих художественных и архитектурных достижений.

Одним из ключевых открытий эпохи Возрождения стало использование геометрических принципов для создания линейной перспективы в живописи. До этого времени картины часто выглядели плоскими, без четкого представления о глубине пространства. Однако в XV веке итальянский архитектор и художник Филиппо Брунеллески (1377–1446) разработал систему линейной перспективы, основанную на геометрических законах.

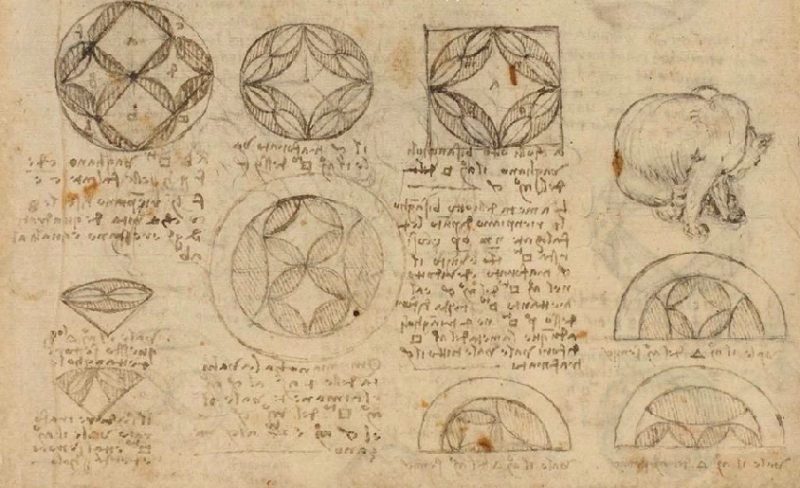
• Леонардо да Винчи (1452–1519) использовал геометрические принципы для создания своих знаменитых картин, таких как «Тайная вечеря» и «Мона Лиза». Он подробно изучал пропорции человеческого тела, создавая идеальные гармоничные формы.
• Альбрехт Дюрер (1471–1528) написал трактат «Руководство к измерению», где подробно описал методы использования геометрии в искусстве. Он также разработал способы построения правильных многоугольников и других сложных фигур.

Ренессансные архитекторы, такие как Леон Баттиста Альберти (1404–1472) и Донато Браманте (1444–1514), использовали геометрические принципы для проектирования зданий. Они стремились к гармонии и симметрии, основывая свои проекты на пропорциях, взятых из классической античной архитектуры.

• Знаменитый собор Санта-Мария-дель-Фьоре во Флоренции, завершенный Филиппо Брунеллески, стал образцом использования геометрии в строительстве. Его огромный купол был спроектирован с учетом сложных геометрических расчетов, что позволило достичь невиданной ранее прочности и красоты.
• Леонардо да Винчи также занимался архитектурными проектами, используя геометрические закономерности для создания идеальных пропорций.

Помимо искусства и архитектуры, геометрия продолжала развиваться как самостоятельная наука. Ученые эпохи Возрождения начали задумываться о более глубоких свойствах пространства и форм. Например:

• Никколо Тарталья (1499–1557) и Джироламо Кардано (1501–1576) исследовали геометрические методы решения алгебраических уравнений.
• Джованни Баттиста делла Порта (1535–1615) изучал оптические явления, используя геометрические принципы.

Период Средневековья и Ренессанса стал временем перехода от античной геометрии к современной науке. Если в Средние века геометрия сохранялась благодаря усилиям арабских ученых, то эпоха Возрождения дала ей новую жизнь. Именно в это время геометрия начала активно применяться не только в теоретических исследованиях, но и в практических областях: искусстве, архитектуре, инженерии и других науках.

Этот этап подготовил почву для революционных открытий XVII века, таких как аналитическая геометрия Рене Декарта, которая окончательно объединила алгебру и геометрию, открыв новые горизонты для математического анализа и физики.

Революция XVII века

XVII век стал революционным для геометрии благодаря созданию аналитической геометрии Рене Декартом. Он предложил использовать алгебраические методы для решения геометрических задач, что открыло новые горизонты в развитии науки. Теперь геометрические фигуры можно было описывать уравнениями, а их свойства исследовать алгебраическими методами.

В XVIII-XIX веках произошло дальнейшее расширение границ геометрии. Была развита проективная геометрия, изучающая свойства фигур, сохраняющиеся при проектировании. Николай Лобачевский и Янош Больяй независимо друг от друга создали неевклидову геометрию, которая существенно расширила представления о пространстве.

Современная геометрия

XX век стал эпохой беспрецедентного расцвета геометрии, когда она перестала быть только теоретической наукой и превратилась в мощный инструмент для решения практических задач. Это время ознаменовалось появлением новых разделов геометрии, которые существенно расширили ее границы и применимость. Рассмотрим ключевые направления и их значение.

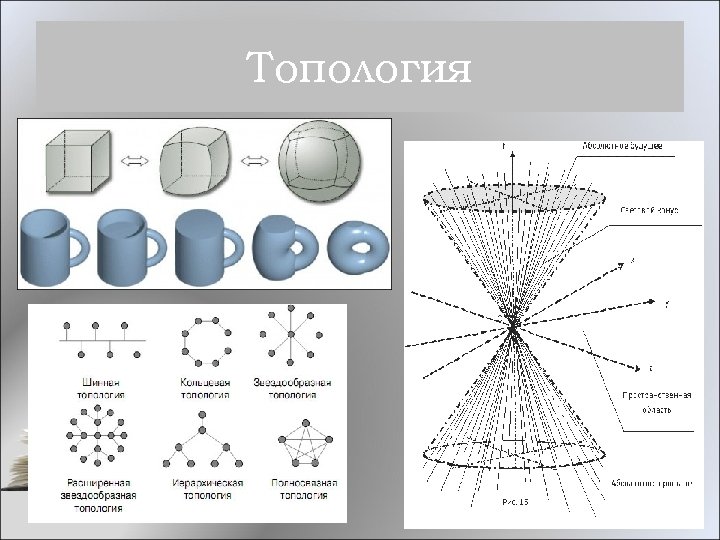
Топология — это раздел геометрии, изучающий свойства фигур, которые остаются неизменными при непрерывных деформациях, таких как растяжение, сжатие или изгибание. В отличие от классической геометрии, топология игнорирует точные размеры и углы, фокусируясь на более общих характеристиках, таких как связность, компактность и число «дырок» в объекте. Топология начала формироваться в XIX веке благодаря работам Георга Кантора и Анри Пуанкаре, но именно в XX веке она стала самостоятельной дисциплиной.  Сегодня топология используется в самых разных областях. Например, в биологии она помогает анализировать структуру ДНК и белковых молекул, а в физике применяется для исследования квантовых явлений, таких как топологические изоляторы. В компьютерной графике топология позволяет моделировать трехмерные объекты и создавать реалистичные анимации. Таким образом, топология стала неотъемлемой частью современной науки и технологий.

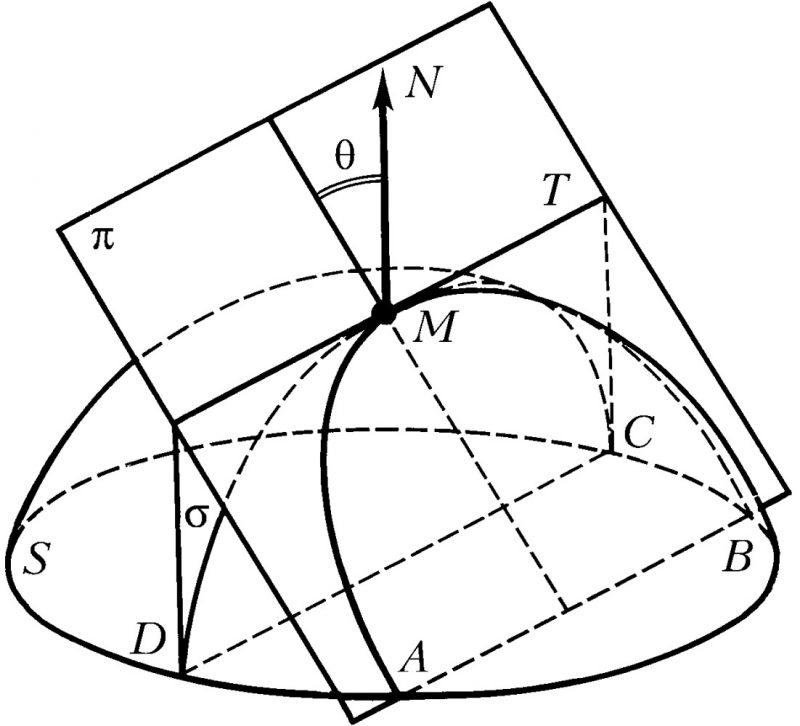
Дифференциальная геометрия изучает гладкие кривые, поверхности и их свойства с использованием методов математического анализа. Она играет ключевую роль в современной физике, особенно в общей теории относительности. Основные понятия дифференциальной геометрии включают кривизну, которая измеряет, насколько кривая или поверхность отклоняется от плоскости, и многообразия — обобщенные пространства, которые локально похожи на евклидово пространство.

Общая теория относительности Альберта Эйнштейна основана на дифференциальной геометрии. Пространство-время рассматривается как четырехмерное многообразие, где гравитация проявляется через искривление этого многообразия. Теория струн также использует сложные многомерные пространства для описания фундаментальных частиц и взаимодействий. В робототехнике дифференциальная геометрия применяется для планирования движений роботов в сложных средах, а в медицине она используется для анализа формы органов и тканей.

Алгебраическая геометрия изучает геометрические объекты, заданные алгебраическими уравнениями. Этот раздел объединяет алгебру и геометрию, позволяя решать сложные задачи с помощью абстрактных методов. Одним из ключевых достижений алгебраической геометрии стала разработка теории схем Александра Гротендика, которая стала основой современной алгебраической геометрии. Благодаря этому разделу удалось решить знаменитую проблему Ферма, над которой математики бились более трехсот лет.

В криптографии алгебраическая геометрия используется для создания безопасных алгоритмов шифрования, а в теоретической физике она помогает исследовать структуру пространства-времени и квантовых полей. Таким образом, алгебраическая геометрия стала важным инструментом как в чистой математике, так и в прикладных науках.

Современные компьютерные технологии открыли новые возможности для применения геометрии. Особенно важны методы геометрического моделирования, которые используются в компьютерной графике и анимации для создания реалистичных трехмерных объектов. Алгоритмы рендеринга основаны на законах оптики и геометрии, что позволяет достичь высокой степени детализации в виртуальных мирах.

Системы автоматизированного проектирования (CAD) также базируются на геометрических принципах. Они позволяют проектировать сложные конструкции, такие как здания, машины и механизмы, с высокой точностью. Фрактальная геометрия, изучающая самоподобные структуры, часто встречающиеся в природе, используется для создания реалистичных текстур и ландшафтов в компьютерных играх и фильмах.

Современная геометрия активно применяется в различных областях науки и техники. В архитектуре и строительстве геометрические принципы используются для проектирования сложных зданий, таких как небоскребы или мосты. Параметрический дизайн, основанный на геометрических алгоритмах, позволяет создавать уникальные формы, которые невозможно было бы реализовать с помощью традиционных методов.

В робототехнике геометрия помогает разрабатывать алгоритмы для управления движением роботов и их взаимодействия с окружающей средой. В медицине геометрические методы применяются для анализа данных томографии и создания трехмерных моделей органов. Это позволяет врачам лучше понимать структуру человеческого тела и планировать сложные операции.

Современная геометрия играет ключевую роль в развитии фундаментальных наук. В физике теория относительности и квантовая механика используют геометрические концепции для описания физических явлений. Теория струн предполагает существование дополнительных измерений пространства, что требует новых геометрических подходов. В космологии исследования формы Вселенной основаны на геометрических моделях, таких как гиперболическая, сферическая или плоская геометрия.

Современная геометрия продолжает развиваться, открывая новые горизонты для науки и технологий. Одним из перспективных направлений является квантовая геометрия, которая изучает пространство на масштабах, где действуют квантовые эффекты. Геометрический искусственный интеллект использует геометрические методы для анализа больших данных и машинного обучения. Биогеометрия исследует геометрические закономерности в живых организмах и экосистемах, что может привести к новым открытиям в биологии и экологии.

Значение геометрии в образовании

История развития геометрии демонстрирует удивительное единство практической применимости и теоретической глубины этой науки. От древних землемеров до современных теоретиков – путь геометрии показывает, как практические потребности человечества привели к созданию одной из самых фундаментальных областей математического знания.

Современные образовательные программы сохраняют важность изучения геометрии, так как она формирует пространственное мышление и логические навыки. Основные геометрические принципы, заложенные еще в «Началах» Евклида, продолжают служить фундаментом математического образования.

Таким образом, история геометрии – это история постоянного развития и совершенствования методов познания пространства. Каждый новый этап в развитии науки добавлял новые инструменты и подходы, но при этом сохранялась преемственность основных принципов, заложенных еще древними цивилизациями.

Сегодня геометрия остается одной из наиболее динамично развивающихся областей математики, продолжающей находить новые применения в различных сферах человеческой деятельности.