Как найти площадь параллелограмма

В школьной геометрии есть множество фигур, с которыми мы знакомимся постепенно — от треугольников и квадратов до более сложных четырёхугольников. Параллелограмм — одна из таких фигур, и хотя его внешний вид может вызывать вопросы, формулы, связанные с ним, весьма логичны и запоминаются легко. В этой статье разберёмся, как находить площадь параллелограмма, почему формула работает именно так и какие есть нюансы при решении задач.

Что такое параллелограмм

Параллелограмм — это четырёхугольник, у которого противоположные стороны попарно параллельны. Это определение уже заложено в самом названии фигуры: «параллел» — параллельные стороны, «грамма» — линия, чертёж. Визуально он может напоминать наклонённый прямоугольник или ромб. Важно, что у параллелограмма противоположные стороны не только параллельны, но и равны по длине.

В школьных учебниках можно встретить такие виды параллелограммов:

• обычный параллелограмм (наклонённая фигура с параллельными сторонами),
• прямоугольник (особый случай, где углы — прямые),
• ромб (все стороны равны),
• квадрат (и углы прямые, и стороны равны — это тоже параллелограмм!).

Зачем нужна площадь

Площадь — это числовое выражение того, сколько места занимает фигура на плоскости. Если у вас есть параллелограмм, например, кусок ткани или участок земли такой формы, вы наверняка захотите узнать, сколько пространства он занимает. И тут приходит на помощь формула площади.

Формула площади параллелограмма

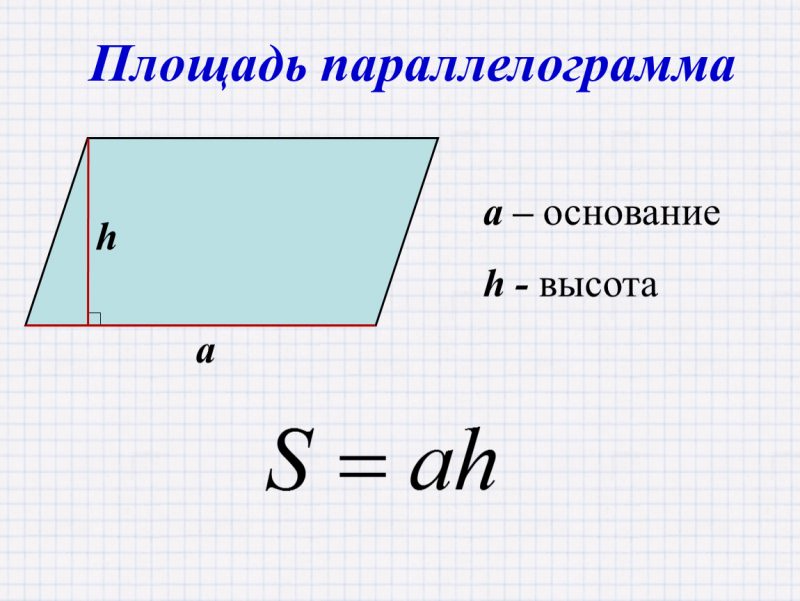
Главная формула, которую стоит запомнить:

S = a × h,
где:

• S — площадь параллелограмма,
• a — длина основания (одной из сторон),
• h — высота, опущенная на это основание.

Формула похожа на формулу площади прямоугольника (S = a × b), но с одним отличием: у параллелограмма высота — это не длина второй стороны, а именно перпендикуляр, опущенный на основание. Иными словами, если фигура «наклонена», то считать площадь по наклонной стороне неверно — нужно найти высоту.

Если разрезать параллелограмм по высоте и переставить отрезанный треугольник к другому краю фигуры, получится прямоугольник с теми же основанием и высотой. Это наглядное доказательство того, что формула площади параллелограмма такая же, как у прямоугольника.

Эта геометрическая «магия» делает параллелограмм понятной и доступной фигурой. Даже если фигура кажется сложной на глаз, логика её площади предельно простая.

Если нет высоты

Иногда в задачах не указывают высоту, а только стороны и угол между ними. В таком случае применяют другую формулу:

S = a × b × sin(α),
где:

• a и b — длины сторон, образующих угол,
• α — угол между ними в градусах или радианах,
• sin(α) — синус угла (можно найти по таблице или с помощью калькулятора).

Эта формула используется, если известны две смежные стороны и угол между ними. Она универсальна, особенно полезна в задачах с тригонометрией или в старших классах.

Пример

Допустим, вы хотите сшить флаг в виде параллелограмма, и у вас есть кусок ткани. Основание — 80 см, высота — 50 см. Площадь будет:
S = 80 × 50 = 4000 см², или 0,4 м².

А теперь представьте, что у вас есть участок земли, форма которого напоминает параллелограмм: стороны по 25 м, угол между ними — 60°. Тогда:
S = 25 × 25 × sin(60°) = 625 × 0,866 ≈ 541,25 м².

Так можно рассчитать любую площадь — главное правильно понять, какие данные у вас есть и какую формулу применить.

В чём могут быть ошибки:

1. Путают сторону и высоту. Важно понимать, что высота — это перпендикуляр, а не просто длина другой стороны.
2. Используют угол между противоположными сторонами. В формуле с синусом нужно использовать угол между смежными сторонами.
3. Неверно рассчитывают синус. Всегда проверяйте, что ваш калькулятор в нужном режиме: градусы или радианы.

Площадь и координаты

Иногда в задачах используется координатная плоскость. Если известны координаты вершин параллелограмма, можно использовать более сложные формулы с определителями. Такие методы обычно проходят в старших классах или на олимпиадах, но они тоже основаны на геометрической логике: через длины и высоты или площади треугольников.

Площадь параллелограмма — тема, которая не просто «проходит» в школьной программе, но действительно пригождается в жизни. Будь то черчение, строительство, кроение или география — понимание, как рассчитать площадь, открывает новые горизонты.

Главное — не бояться фигуры, даже если она наклонена или кажется сложной. За параллелограммом скрывается простая формула и логика, доступная каждому. Поняв один раз, вы сможете применять знания в самых разных ситуациях. А если понадобится — онлайн-калькулятор всегда под рукой, чтобы сверить результат.

Рекомендуем по теме

Как считать разницу в процентах и не попасться на уловки